Gliederung

1.  Ein Fraktal - was ist das?

Der Begriff Fraktal wurde von Benoit B. Mandelbrot 1980 eingeführt. Er leitet sich ab vom lateinischen Wort fractus, gebrochen. Schon Anfang dieses Jahrhunderts beschäftigten sich die französischen Mathematiker Pierre Fatou und Gaston Julia mit rückgekoppelten Gleichungen. Sie mußten davor aber schließlich kapitulieren, da sie damals noch keine Computer zur Verfügung hatten. Das Berechnen der sogenannten Mandelbrot-Menge ist schon in der Übersicht so aufwendig, daß ein menschlicher Rechenknecht Jahre für die Berechnung bräuchte. Erst durch die modernen Rechenmaschinen sind die Fraktale handhabbar geworden. Auf diesen Umstand ist es wohl an erster Stelle zurückzuführen, daß ihre Entdeckung und weitere Erforschung so lange hat auf sich warten lassen.

Fast jeder hat in irgendeiner Form schon einmal ein Fraktal gesehen, bewußt oder unbewußt. Aber es ist nicht ganz einfach, zu beschreiben, was ein Fraktal denn nun wirklich ausmacht, wann eine Grafik eine „fraktale Grafik“ ist.

1.1  Die Mittleres-Drittel Cantor-Menge

Wir wollen dazu eines der am einfachsten zu konstruierenden und am besten bekannten Fraktale betrachten, die Mittleres Drittel-Cantor-Menge. Trotz ihrer Einfachheit zeigt diese Menge viele typische fraktale Charakteristika. Erzeugt wird sie aus dem Einheits- Intervall [0,1] (das ist die Menge aller zwischen 0 und 1 liegenden Zahlen) durch eine Reihe von Entfernungs-Operationen:

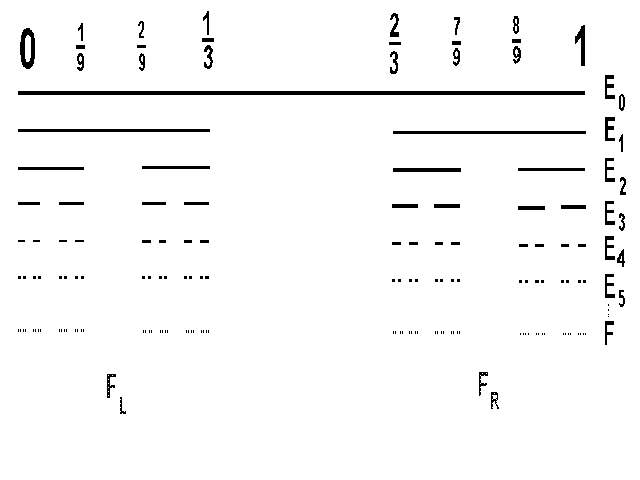
Sei E₀ das Intervall [0,1]. Man erhält die Menge E₁ durch Entfernen des mittleren Drittels von E₀. Damit besteht E₁ aus den beiden Intervallen [0, 1/3] und [2/3, 1] (siehe Abbildung).

Erneutes Entfernen der mittleren Drittel von E₁ ergibt E₂, bestehend aus den vier Intervallen [0, 1/9], [2/9, 1/3], [2/3, 7/9] und [8/9, 1]. Auf diese Art und Weise kann man nun immer weiter fortfahren: E₃ entsteht aus E₂, E₄ aus E₃, E₅ aus E₄ oder allgemein ausgedrückt entsteht E_k aus E_{k - 1}. Es läßt sich leicht nachvollziehen, daß E_k aus 2^k Intervallen besteht und diese Intervalle die Länge 3^{- k} (= 1/(3^k)) haben:

Die zugehörige Cantor-Menge, wir wollen sie mit F bezeichnen (siehe Abbildung oben), entsteht dann, wenn die k sehr groß werden (gegen unendlich streben). Es ist einsichtig, daß F selbst niemals gezeichnet werden kann mit seiner infinitesimalen (d.h. im Grenzübergang unendlich kleinen) Struktur. „Bilder von F“ werden deshalb immer nur Bilder einer der „Vorstufen“ E_k sein, was für große k aber eine gute Näherung ist.

Auf den ersten Blick mag es nun erscheinen, daß vom Intervall [0,1] während der Konstruktion der Menge F soviel entfernt worden ist, daß nichts mehr davon übrig geblieben ist. In der Tat enthält F unendlich viele Zahlen in der Nachbarschaft von jedem ihrer Punkte.

Hier nun einige der (mathematischen) Eigenschaften der Mittleres Drittel-Cantor-Menge F:

• F ist selbstähnlich. Es ist sofort einzusehen, daß der Teil von F im Intervall [0, 1/3] und der Teil im Intervall [2/3, 1] geometrisch F ähnlich sind: sie sind eine Verkleinerung von F im Maßstab 1:3. Genauso sind die vier Teile von E₂ ähnlich F, nur im Maßstab 1:9. Die sechzehn Teile von E₃ sind F ebenfalls ähnlich im Maßstab 1:27, usw. Die Cantor-Menge enthält also Kopien von sich selbst in immer kleineren Maßstäben.
• F besitzt eine „Feinstruktur“: sie enthält Details in beliebig kleinen Maßstäben. Je stärker das Bild der Cantor-Menge vergrößert wird, desto mehr Löcher werden sichtbar.
• Man erhält F mittels einer rekursiven Vorgehensweise: die Konstruktion basiert auf der wiederholten Entfernung des mittleren Drittels der Intervalle. Aufeinander folgende Schritte ergeben ein immer feineres Bild und damit immer bessere Näherungen E_k der Menge F.
• Die Geometrie von F kann man nicht einfach auf klassische Weise beschreiben: weder genügen die geometrischen Orte der Punkte einfachen geometrischen Bedingungen, noch tut es die Menge von Lösungen einer einfachen Gleichung.
• Es ist unpraktisch, die lokale Geometrie von F beschreiben zu wollen, da in der Umgebung eines jeden Punktes eine große Zahl anderer Punkte liegt, voneinander getrennt durch verschieden große Löcher.
• Obwohl F in gewisser Weise eine sehr große Menge ist (sie enthält ja unendlich viele Punkte), kann ihre Größe nicht mit den uns vertrauten Maßen, z.B. der Länge, angegeben werden. F hat, wenn man es so ausdrücken möchte, die Länge Null.

Ein weiteres Beispiel für ein „echtes Fraktal“ (im strengen mathematischen Sinn) ist z.B. das Sierpinski-Dreieck, dessen erste Vorstufen im folgenden Bild gezeigt werden:

1.2  Rückgekoppelte Prozesse

Die Grafiken, um die es hier geht, beruhen auf sogenannten rückgekoppelten Prozessen. Diese sind in den Naturwissenschaften schon lange bekannt, z.B. Räuber-Beute-Beziehungen in der Ökologie, die Kinetik chemischer Reaktionen, Wettervorhersage oder Differenzengleichungen in der Mathematik.

Von einem vorgegebenen Startwert ausgehend wird eine Rechenvorschrift wiederholt angewendet, um einen zukünftigen Zustand des Systems zu berechnen:

Der Startwert z₀ wird auf die Rückkopplungsgleichung f (z_n,c) (2.a) angewendet, wobei z.B.

sein kann. Das Ergebnis ist dann z_n+1, das wiederum in die Gleichung für z eingesetzt wird. In Abhängigkeit von Startwert und Konstante c entwickelt sich nun die Rückkopplung.

Die folgende Tabelle enthält Beispiele für die Entwicklung der Rückkopplung mit Gleichung (1.2.b) für verschiedene Startwerte z₀ und der Konstanten c:

Für z₀ > 1, c = 0 gehen die z_n sehr schnell gegen unendlich. Man sagt auch: unendlich ist der Attraktor der Rückkopplung. Für z₀ < 1, c = 0 werden die Werte immer kleiner, Null ist hier der Attraktor. Wird z₀ = 1, c = 0 gewählt, bleibt z_n konstant gleich 1. Diese Sequenz liegt genau auf der Grenze zwischen den beiden Domänen der Attraktion, unendlich und Null.

Ist die Konstante c von Null verschieden, so kann man oftmals zunächst nicht entscheiden, auf welchen Attraktor die Rückkopplung zuläuft oder ob sie zwischen zweien (wie im dritten Beispiel) hin- und herpendelt.

Im allgemeinen ist bei dieser einfachen Rückkopplungsgleichung jedoch recht schnell zu erkennen, wohin die z_n-Werte laufen. Bei anderen Gleichungen, z.B. Differentialgleichungen, ist das aber oft nicht der Fall. Hier entscheiden schon kleinste Unterschiede in den Anfangsbedingungen, ob sich das System auf einen endlichen Attraktor zubewegt, auf unendlich zuläuft oder vielleicht zwischen mehreren Attraktoren pendelt (Beispiel Verhulst-Dynamik .

Für rückgekoppelte Prozesse ist es auch gleichgültig, ob in diskreten Schritten (in der Ökologie z.B. die Veränderung einer Population von einer Generation zur nächsten) oder quasikontinuierlich in infinitesimalen Schritten (z.B. viele Aufgabenstellungen in Mathematik oder Physik) gerechnet wird. Bei manchen Problemen, z.B. in der Reaktions-Kinetik, kann man die Schrittweite auch mehr oder weniger groß bzw. klein wählen, ohne daß sich wesentliches am Ergebnis ändert.

Besonders interessant werden die Grafiken, wenn man den Bereich der reellen Zahlen verläßt und auf den Wertebereich der komplexen Zahlen übergeht. D.h., die Grafiken entstehen als Bilder in der komplexen Zahlenebene mit der horizontalen reellen Achse und der vertikalen imaginären Achse. Aus dem Übergang von den reellen zu den komplexen Zahlen erwächst nun eine ungeheure Mannigfaltigkeit an Formen und die diesen Grafiken innewohnende Ästhetik, die die Bilder auch für Nicht-Mathematiker so anziehend machen.

1.3  Selbstähnlichkeit

Hierunter versteht man das Phänomen, daß bei wiederholten Ausschnittvergrößerungen die gleichen Strukturen immer wieder auftreten. So taucht z.B. bei der Mandelbrot-Menge der große Hauptkörper, das sogenannte Apfelmännchen, auch in kleinerer Form immer wieder auf. Oder, vergrößert man den Rand von Julia-Mengen, so bleibt die (oftmals schrumpelige) Struktur immer erhalten. Das besondere bei den Fraktalen, einem Begriff, den Benoit B. Mandelbrot hierfür eingeführt hat, ist nun, daß selbst unendlich-fache Vergrößerungen möglich sind, ohne daß die fraktale Struktur verloren geht.

In der Natur tritt das Phänomen der Selbstähnlichkeit auch auf, aber in der Regel nur in „beschränkterem“ Maße, da ja keine unendlichen Vergrößerungen angefertigt werden können. Man denke z.B. an die Verzweigung eines Baumstammes in größere und kleinere Äste und weiter in Zweige oder die Bildung von großen Flußsystemen aus kleinsten Rinnsalen, Bächen, Flüssen und Strömen. Mandelbrot selbst führt das Beispiel der sich immer weiter verzweigenden, länger werdenden und immer mehr Details freigebenden Küstenlinie einer Insel beim Vergrößern an.

Sogar in der Kunst tritt Selbstähnlichkeit auf ! Man denke nur an die hoch-interessanten Grafiken M. C. Eschers. Einige seiner Bilder sind sogar im strengen mathematischen Sinne Fraktale, wie z.B. „Kreislimit IV (Himmel und Hölle)“, das Teufel in schwarz und Engel in weiß zeigt. Von der Mitte zum Rand hin werden die Figuren immer kleiner und werden dort „unendlich“klein :

1.4  Die Mandelbrot-Menge

1980 entdeckte der amerikanische Mathematiker Benoit B. Mandelbrot die nach seinem Namen benannte Menge. Ihr liegt die folgende einfache Rückkopplung

in der komplexen Zahlenebene zugrunde. Sie liefert - vor allem in ihren Ausschnittvergrößerungen - mit die interessantesten Grafiken überhaupt.

Zur Berechnung werden z_n in Realteil X und Imaginärteil Y sowie c in a + ib (i: imaginäre Einheit) getrennt. Aus (1.4.a) ergeben sich dann die beiden Gleichungen

Die Startwerte x₀ und y₀ werden auf Null gesetzt, a und b spannen den Ausschnitt der komplexen Zahlenebene auf, aus dem das Bild gerechnet wird. Mit anderen Worten: für jedes Pixel, aus dem die Grafik der Mandelbrot-Menge zusammengesetzt wird und das durch den Punkt mit den Koordinaten (a, b) bestimmt wird, werden die obigen Rückkopplungsgleichungen gerechnet, jeweils mit x₀ = 0 = y₀.

Es existieren zwei Attraktoren, unendlich und ein endlicher Attraktor. Die Mandelbrot-Menge besteht nun aus den Werten von c = a + ib, für die die Rückkopplung nicht divergiert, sie also auf den endlichen Attraktor zuläuft. Diese Punkte färbt das Programm schwarz ein. Weiß werden dagegen alle die Punkte der komplexen Zahlenebene eingefärbt, die „unendlich“ als Attraktor haben, also nicht zur Menge gehören.

Hier taucht nun das kleine Problem auf, daß auch der schnellste Computer unendlich lange bräuchte, um bis „unendlich“ zu rechnen. Dem leistet man dadurch Abhilfe, daß man einen Grenzwert für die Maximalzahl an Iterationen vorgibt. Sobald diese Iterationstiefe erreicht ist, wird dieser Punkt als zum Attraktor unendlich zugehörig eingefärbt. Daraus erwächst die neue Schwierigkeit, die maximale Iterationszahl nicht zu hoch und nicht zu niedrig zu wählen. Gerade wenn man sich in den Randbereichen der Menge befindet, darf kein zu niedriger Wert gewählt werden, weil das Bild sonst „unscharf“ und „verschmiert“ erscheint. In diesem Fall werden Punkte als zur Menge gehörig betrachtet, die eindeutig nicht dazu gehören. Andererseits erhöhen hohe Werte für die Iterationstiefe die Rechenzeit. Hier können nur Anhaltspunkte für eine geeignete Wahl dieses Parameters gegeben werden. Am sichersten ist es immer, mehrere Rechnungen mit verschiedener Iterationstiefe durchzuführen.

Die Mandelbrot-Menge ist zusammenhängend, d.h. jeder Punkt der Menge kann von jedem beliebigen anderen Punkt der Menge erreicht werden, ohne die Menge dabei verlassen zu müssen. Auch die Satelliten-Apfelmännchen, die scheinbar vom Hauptkörper losgelöst sind, sind in Wirklichkeit durch dünnste Fäden mit ihm verbunden, wie die Mathematiker beweisen konnten. Es gibt nur eine einzige Mandelbrot-Menge zur Rückkopplungsgleichung (1.4.a), im Gegensatz zu unendlich vielen Julia-Mengen zu (1.4.a). Die Mandelbrot-Menge ist symmetrisch zur reellen Achse, weshalb es bei den Berechnungen zwecks Rechenzeitersparnis sinnvoll ist, diese Symmetrie auszunutzen.

Es lassen sich auch kompliziertere Gleichungen als (1.4.a) verwenden. Dann entstehen andere Figuren (mit zum Teil anderen Symmetrien), die aber prinzipiell die gleichen Eigenschaften besitzen. Wenn man von „der Mandelbrot-Menge“ spricht, bezieht man sich aber im allgemeinen immer auf die Grafiken, welche mittels der Rückkopplungsgleichung (1.4.a) erzeugt wurden.

Mehr zur Mandelbrot-Menge und ein paar Bilder

1.5  Die Julia-Mengen

Den Julia-Mengen liegt die gleiche Rückkopplungsgleichung zugrunde wie der Mandelbrot-Menge :

Allerdings wird hier die Konstante c = a + ib vor Beginn der Rechnung festgelegt und die x_n- und y_n-Werte spannen die Ebene auf, in der gerechnet wird:

Auch hier gehören alle die Punkte der komplexen Zahlenebene zur Menge, die einen endlichen Attraktor besitzen. Diese Punkte werden bei diesem Mengentyp aber aus programmtechnischen Gründen standardmäßig weiß eingefärbt. Alle Punkte mit dem Attraktor „unendlich“ werden schwarz eingefärbt.

Das besondere an diesem Mengentyp ist, daß die Menge zu jedem c eine andere Struktur besitzt. Besonders interessante Formen ergeben sich, wenn c in der Nähe des Randes der Mandelbrot-Menge liegt. Wird der Wert für c aus dem Inneren der Mandelbrot-Menge gewählt, so ist die Julia-Menge zusammenhängend. Hingegen spaltet sich die Julia-Menge in unendlich viele Teile, sobald c außerhalb der Mandelbrot-Menge gewählt wird (die Julia-Menge zerfällt in eine sogenannte Cantor-Menge).

Die Julia-Mengen sind wegen der quadratischen Rückkopplungsgleichung um den Drehwinkel 180^° drehsymmetrisch zum Ursprung. Für b = 0 sind sie darüber hinaus symmetrisch zur reellen und imaginären Achse.

Vergrößert man den Rand der Julia-Mengen, so treten immer wieder die gleichen Strukturen auf. Dabei ist es gleichgültig, wie stark vergrößert wird. Das bedeutet, daß die Julia-Mengen selbstähnlich, also Fraktale, sind.

Wie auch schon bei der Mandelbrot-Menge, können auch zur Generierung von Julia-Mengen andere Rückkopplungsgleichungen als (5.a) verwendet werden. Da diese Rückkopplungsgleichungen nicht mehr einfach quadratisch sind, ergeben sich für die Grafiken auch andere Symmetrien. Je nach verwendeter Gleichung sind die Mengen der „Standard“-Julia-Menge nach (5.a) wiederum ähnlich oder auch total verschieden.

Ein paar Julia-Mengen

1.6  Biomorphe

Die Bezeichnung Biomorphe stammt daher, daß die mit diesem Verfahren erzeugten Grafiken Einzellern (Bakterien u.a.) sehr ähnlich sehen. „Entdeckt“ wurden die Biomorphe von Clifford A. Pickover, einem Wissenschaftler am Thomas-J.-Watson-Forschungßentrum der IBM in Yorktown Heights.

Es werden dieselben Rückkopplungsgleichungen verwendet, wie für die Julia-Mengen. Auch hier muß die komplexe Konstante c vor Beginn der Rechnung vorgegeben werden. Der Unterschied besteht im verschiedenen Abbruchkriterium: entweder wird nach einer bestimmten Zahl von Iterationen die Rückkopplung beendet (wie bei den anderen Mengen auch) oder wenn der Real- oder Imaginärteil betragsmäßig (d.h., das Vorzeichen wird nicht beachtet) größer als eine vorzugebende Schranke ist. Wenn einer dieser beiden Beträge kleiner als die Schranke ist, wird das entsprechende Pixel schwarz eingefärbt, ansonsten wird der Bildpunkt in Abhängigkeit der durchgeführten Iterationen nach der aktuellen Farbpalette gefärbt.

Ein paar Biomorphe gefällig ? :-)

1.7  Das Newton-Verfahren für komplexwertige Funktionen

Schon in der Mittelstufe lernt man im Mathematikunterricht sogenannte quadratische Gleichungen zu lösen, z.B.

Die Lösungsformel für quadratische Gleichungen

liefert für das obige Beispiel sofort

Die Formel liefert alle (reellen) Lösungen und diese sind auch exakt. Für kompliziertere Gleichungen gibt es keine Lösungsformeln mehr. Will man auch sie lösen, so ist man auf Näherungsverfahren angewiesen, z.B. auf das nach dem englischen Mathematiker Newton.

Ausgehend von einem Punkt der Kurve geht man auf der Tangente in diesem Punkt bis zum Schnittpunkt mit der X-Achse. Von dort zieht man die Senkrechte bis zum Schnittpunkt mit der Kurve. An diesem neuen Punkt wird wieder eine Tangente angelegt, der Schnittpunkt mit der X-Achse gesucht usw. Auf diese Weise nähert man sich (zumindest in den meisten Fällen) einer Nullstelle der Funktion. In der Abbildung unten ergeben sich die Nullstellen X_a und X_b, wenn man von den Punkten A bzw. B startet. Man sagt auch A wird von X_a angezogen oder Xa ist der Attraktor von A (entsprechend für B).

Alle Punkte der Kurve links vom Hochpunkt werden von dem Attraktor X_a angezogen, alle Kurvenpunkte rechts vom Hochpunkt entsprechend von der Nullstelle X_b. Der Hochpunkt selber hat keine Tangente, die die X-Achse schneidet. Für ihn ist nicht entscheidbar, von welchem Attraktor er angezogen wird.

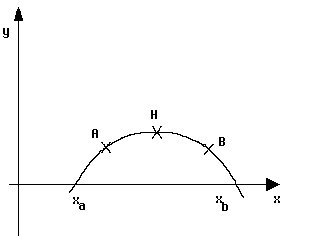
Entsprechend ihrem Attraktor können nun die Kurvenpunkte verschieden eingefärbt werden. Interessant wird es auch hier aber wiederum erst, wenn man Funktionen mit höherem Grad als 2 wählt und in die komplexe Zahlenebene geht.

Die einfachste Rückkopplungsgleichung für das Newton-Verfahren für komplexwertige Funktionen sieht nun schon etwas komplizierter aus als für die oben beschriebenen Mengen und braucht auch wesentlich länger für die Berechnung. Die Grundgleichung lautet

Daraus ergibt sich die folgende Rückkopplung

Nach Aufspaltung in Real- und Imaginärteil erhält man die Gleichungen

Die Nullstellen von (1.7.d) errechnen sich zu

Ein Punkt der Ebene wird nun in der Farbe a (b, c) eingefärbt, wenn die Rückkopplung auf den Attraktor z_a (z_b, z_c) zuläuft. Die Punkte, für die nach einer vorgegebenen Anzahl an Iterationen nicht entscheidbar ist, auf welchen Attraktor sie zulaufen, werden schwarz eingefärbt.

Auch hier tritt das kleine Problem der endlichen Genauigkeit des Computers auf. Bei den unter 1.4 bis 1.6 besprochenen Mengen ist das zweite Abbruchkriterium nach der Iterationszahl der Abstand vom Ursprung des Koordinatensystems. Beim Newton-Verfahren ist es der Abstand von den Nullstellen. Je kleiner der Wert des hierfür zuständigen Parameters gewählt wird, desto genauer wird die Berechnung und desto schärfer wird das Bild. Da die Berechnung der Newton-Rückkopplung aber durch ihre kompliziertere Struktur recht viel Zeit benötigt, empfehlen sich zum Testen kleine Werte für den Abstand, z.B. 0.1. Bei Ausschnittvergrößerungen muß dann natürlich genauer gerechnet werden.

Da sich einerseits durch die komplizierteren Rückkopplungsgleichungen längere Rechenzeiten ergeben als für die übrigen Mengentypen und andererseits große Bildteile schwarz eingefärbt werden, wird beim Newton-Verfahren das gerade in Rechnung befindliche Pixel durch einen weißen Punkt gekennzeichnet. Dies erleichtert die Verfolgung des Fortschreitens der Rechnung.

Ein paar Grafiken zum Newton-Verfahren

1.8  Geschwindigkeitsdiagramme

Außer einer Einteilung der Punkte der komplexen Zahlenebene in die zwei Klassen

a)

zur Menge gehörig

b)

nicht zur Menge gehörig

Bei den Geschwindigkeitsdiagrammen wird ein Punkt in Abhängigkeit von der Zahl der Iterationen eingefärbt, die notwendig sind, um einen ebenfalls vorzugebenden Abstand G vom Ursprung (nicht von der Menge!) zu überschreiten. Je weiter ein Punkt vom Ursprung entfernt ist, desto schneller (nach weniger Iterationen) erreicht bzw. überschreitet er den vorgegebenen Grenzabstand. Nach der Zahl der durchgeführten Iterationen wird dann die Farbe aus der Palette ausgewählt. Alle Punkte mit gleicher Farbe haben damit auch denselben Abstand vom Ursprung.

Der Abstand G vom Ursprung errechnet sich nach

Um Rechenzeit zu sparen, wird die Wurzel bei der Entscheidung, ob ein Punkt diesen Grenzabstand überschritten hat, nicht berücksichtigt. Dies macht für den Rechengang keinen prinzipiellen Unterschied.

Zur Verdeutlichung wollen wir als Beispiel die Entwicklung der Mandelbrot-Rückkopplung

für verschiedene Startwerte a und b betrachten:

Als Grenzabstand sei 10 vorgegeben. Wie unschwer zu erkennen ist, wird der Wert 10 bei den Startwerten a = 0.4, b = 0.4 nach der zehnten Iteration überschritten. Im Falle von a = 0.5, b = 0.5 erfolgt dies nach fünf Iterationen. Werden a = 0.5 und b = 0.7 gewählt, wird der Grenzabstand schon nach vier Iterationen und bei a = -2.0, b = 0.5 sogar schon nach der dritten Iteration überschritten.

Die Farbpalette sei folgendermaßen belegt:

Dann wird der Punkt mit den Koordinaten a = 0.4, b = 0.4 braun eingefärbt, das Pixel mit den Koordinaten a = 0.5, b = 0.5 wird mit grau eingefärbt. Entsprechend werden die anderen beiden Punkte orange bzw. gelb gefärbt.

Allerdings gibt es dazu oftmals die kleine Einschränkung, daß Fraktal-Programme „nur“ maximal 256 Farben gleichzeitig auf dem Bildschirm darstellen können. Werden mehr als 255 verschiedene Abstände ermittelt (die 256ste Farbe wird ja für die Menge selbst gebraucht), so wiederholen sich die Farbwerte.

Nach Peitgen und Richter (1986) entsprechen die Geschwindigkeitslinien Äquipotentiallinien, die sich ausbilden würden, wenn auf die Menge eine elektrische Ladung aufgebracht würde.

2  Bestimmung der Dimension (eines Fraktals)

Ein wichtiger Begriff ist der der Dimension. Wir sind gewohnt im täglichen Leben mit den drei topologischen Dimensionen D = 1,2,3 umzugehen. Dabei gibt es den folgenden einfachen Zusammenhang zwischen der Anzahl Stücke a, aus denen ein Objekt zusammengesetzt wird, dem Reduktionsfaktor s und der Dimension D:

Gleichung (2.a) läßt sich nun auch nach D umstellen:

wobei wir D jetzt als Selbstähnlichkeits-Dimension bezeichnen wollen. Für Linie, Quadrat und Würfel ergeben sich also die Selbstähnlichkeits-Dimensionen zu 1, 2 und 3.

Die folgende Tabelle stellt nun die mit (3.b) ermittelten Selbstähnlichkeits-Dimensionen der weiter oben vorgestellten Fraktale zusammen:

D ist nun nicht mehr ganzzahlig. Bei Fraktalen macht es deshalb auch wenig Sinn von Länge, Fläche oder Volumen zu sprechen. Sie werden am besten durch Angabe ihrer Selbstähnlichkeits-Dimension charakterisiert.

An dieser Stelle sei der Vollständigkeit halber auch die Hausdorff-Dimension erwähnt. Die historischen Wurzeln von Mandelbrots fraktaler Dimension liegen in Hausdorffs Arbeit von 1918, obwohl seine Definition der sog. Hausdorff-Dimension nicht besonders praktikabel zu handhaben ist. Schon in elementaren Beispielen ist sie schwierig zu berechnen und bei physikalischen Objekten ist es so gut wie unmöglich sie zu bestimmen.

2.1  Box Counting-Methode

Am einfachsten ist die Dimension physikalischer Objekte zu bestimmen, in dem man sie ganz mit Kästchen der Kantenlänge l einhüllt. Die Länge einer Linie ergibt sich dann aus

wobei N_box(l) die Anzahl der Kästchen bezeichnet, die benötigt werden, um das Objekt ganz zu bedecken.

Entsprechend ergibt sich die Fläche eines Objektes zu

Je kleiner die Kantenlänge l gewählt wird, desto genauer können die Länge oder die Fläche oder das Volumen gemessen werden. Sie werden aber bei nicht-fraktalen Objekten auf jeden Fall einem endlichen Wert zustreben.

Haben wir es dagegen z.B. mit einer fraktalen Kurve zu tun, werden die ganz feinen Unregelmäßigkeiten ein Verhalten N_box(l) µ l^-1 für immer kleiner werdendes l verhindern; die Kurve hat keine endliche Länge. Hier ergibt sich also ein Verhalten N_box(l) µ l^-D, wobei D die fraktale Dimension der Kurve ist.

Ist D = 1,2,3, so wird das System als euklidisch oder nicht-fraktal bezeichnet. Ist D dagegen rational, wird das System als fraktal bezeichnet.

Es gilt folgende Ungleichung:

Eine fraktale Kurve hat die Länge unendlich und die Fläche Null; deshalb sind Begriffe wie Länge, Fläche oder Volumen nur für euklidische Objekte (D = 1,2,3) angebracht.

2.2  Kugel-Methode

Die Box Counting-Methode überschätzt fast immer Länge, Fläche und Volumen. Deshalb ist es günstiger, das Objekt mit Kugeln des Radius r zu bedecken:

und

Der Faktor [3 /2] Ö3 in dem Ausdruck für die Fläche (2.2.b) rührt daher, das eine Fläche am besten so mit Kreisen bedeckt wird, daß man sie zunächst mit regelmäßigen Sechsecken parkettiert und dann diese Sechsecke mit einem Kreis umschreibt.

Ein physikalisches Objekt wird dann als Fraktal bezeichnet, wenn es nicht möglich ist, einen endlichen Wert für seine Länge, Oberfläche, Volumen mit d, d - 1, etc. dimensionalen Hyperbällen (Würfeln) zu erhalten, wenn der Radius (die Kantenlänge) über mehrere Größenordnungen verändert wird.

3  Experiment und Computersimulation

3.1  Elektrochemische Abscheidung und DLA

Fraktale Strukturen treten in der Chemie vor allem bei zufallsmäßigen dendritischen Wachstumsprozessen auf. Folgendes Experiment demonstriert dies:

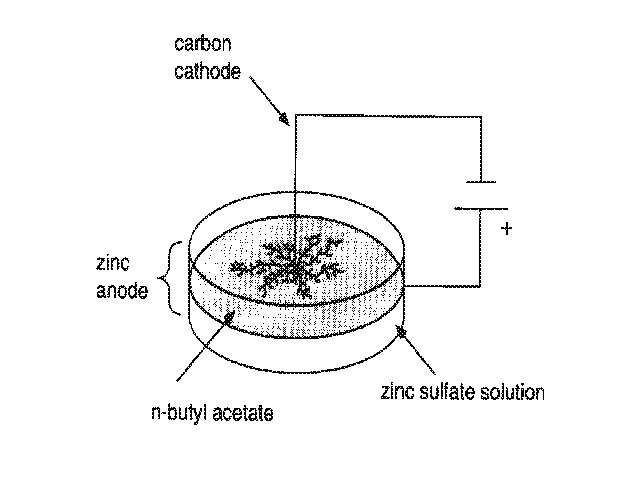
In ein 10 cm hohes Becherglas des Durchmessers 15 cm wird eine 2 molare wäßrige Zinksulfatlösung gegeben. Diese wird mit Butylacetat überschichtet. Als Anode dient ein ringförmiges Zinkblech, als Kathode fungiert eine Bleistiftmiene von 0,5 cm Durchmesser in der Mitte des Becherglases. Die Miene wird soweit eingetaucht, daß sie gerade die Grenzschicht berührt. Sodann wird eine Gleichspannung von ca. 5 Volt angelegt. Im Verlauf von mehreren Minuten wächst nun entlang der Grenzschicht von der Kathode nach allen Seiten hin ein Zinkkristall mit dendritischer Sruktur.

Die fraktale Dimension solcher Kristalle wurde berechnet zu D = 1.66±0.03, was in guter Übereinstimmung mit Computersimulationen steht.

3.2  DLA - Diffusion Limited Aggregation

Die Methode der DLA wurde von Witten und Sander 1981 eingeführt. Sie ist bis jetzt das wichtigste Aggregationsmodell und bietet eine einfache Basis zum Verstehen und Beschreiben von zufallsbedingten dendritischen Wachstumsprozessen.

Die Simulation läuft folgendermaßen ab: In der Mitte des Bildschirms bzw. des Feldes wird ein Keim plaziert. Dann wird vom Rand von zufällig ausgewählter Positionen ein Teilchen gestartet. Dieses bewegt sich nach Zufallszahlengenerator innerhalb des Feldes. Kommt es in direkte Nachbarschaft zum Keim, so lagert es sich an diesen an. Nun wird das nächste Teilchen vom Rand eingesetzt . . .

Die folgende Abbildung zeigt einen solchen DLA-Cluster aus 15000 aggregierten Teilchen.

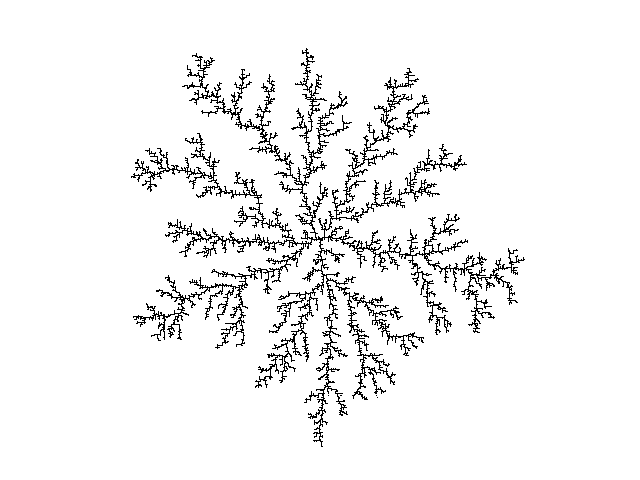
Die fraktale Dimension solcher DLA-Cluster liegt typischerweise zwischen 1.7 und 1.8. Bestimmt wird die fraktale Dimension hierbei günstigerweise so, daß Kreise um das Zentrum (den Urkeim) gelegt werden und nun die innerhalb dieser Kreise liegenden Teilchen gezählt werden. Aus der Steigung der Ausgleichsgeraden einer doppelt-logarithmischen Auftragung der Anzahl Teilchen pro Kreis gegen den Radius kann dann die fraktale Dimension bestimmt werden.

4  Hele-Shaw-Zelle

Die Hele-Shaw-Zelle besteht aus zwei planen Glasscheiben der Stärke 0,5cm und 30cm bzw. 35cm Kantenlänge mit jeweils einem Rand. Sie werden durch dünne Metallfolien als Abstandshalter getrennt. Zwischen die Glasplatten wird eine viskose Flüssigkeit gegeben. In der oberen Scheibe ist in der Mitte ein Loch, durch welches nun Luft gepreßt wird. Dadurch wird die Flüssigkeit zwischen den Scheiben auseinander gedrückt. Dabei bilden sich wiederum fraktale Strukturen - je nach Viskosität der verwendeten Flüssigkeit.

Bei dem folgenden Bild wurde zum Zwecke der Demonstration ein Tropfen mittelviskoses Öl auf eine 10cm x 10cm große Glasplatte aufgebracht und dann eine gleichgrße Glasplatte von Hand daraufgelegt und angepreßt. Dann wurden die beiden Glasplatten möglichst senkrecht voneinander getrennt. Dabei entsteht das fraktalähnliche Muster:

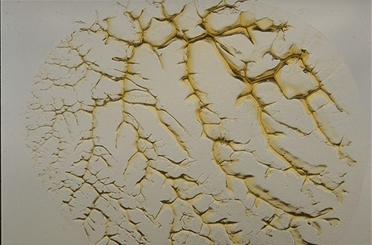
Horváth et.al. haben sogar ein Phasendiagramm der beobachteten Strukturen aufgestellt.

5  Literatur

Mandelbrot- und Julia-Mengen:

• H.-O. Peitgen, P.H. Richter, The Beauty Of Fractals, Springer-Verlag, 1986
• B.B. Mandelbrot, The Fractal Geometry of Nature New York, 1983
• Uwe Beck, Computergrafik, Birkhäuser Verlag, 1988

Fraktale und Chemie:

• D. Avnir (Editor), The Fractal Approach To Heterogeneous Chemistry, John Wiley & Sons, 1989
• T. Vicsek, Fractal Growth Phenomena, World Scientific, 1989
• M. Matsushita, M. Sano, Y. Hayakawa, H. Honjo, Y. Sawada, Fractal Structures of Zinc Metal Leaves Grown by Electrodeposition, Phys. Rev. Lett., 53, 286 (1984)
• V. Horváth, T. Vicsek, J. Kertész, Phys. Rev., A35, 2353 (1987)

Allgemeines zum Thema Fraktale:

• Brian H. Kaye, A Random Walk Through Fractal Dimensions, Verlag Chemie, Weinheim, 1989
• H.-O. Peitgen, H. Jürgens, D. Saupe Chaos and Fractals - New Frontiers of Science, Springer Verlag, 1992
• Walter Seifritz, Wachstum, Rückkopplung und Chaos, Verlag Hanser, München 1987
• J.L. Locher (Hrsg.), Leben und Werk M.C. Escher, Rheingauer Verlagsgesellschaft, Eltville am Rhein 1986
• H.-O. Peitgen, P,H. Richter, Harmonie in Chaos und Kosmos, Bremen, 1984
• H.-O. Peitgen, P,H. Richter, Morphologie komplexer Grenzen, Bremen, 1984

Mathematisch orientierte Bücher bzw. Artikel:

• Kenneth J. Falconer, Fractal Geometry, Mathematical Foundations and Applications, John Wiley and Sons, 1990
• Robert L. Devaney, Linda Keen, Editors, Chaos and Fractals, The Mathematics Behind the Computer Graphics, Proceedings of Symposia in Applied Mathematics, Vol. 39, American Mathematical Society, Providence, Rhode Island, 1988
• G. Julia, Sur l'iteration des fonctions rationnelles, Journal de Math. Pure et Appl. 8, 42-245, 1918

Zurück zu Naturwissenschaften und mathematische Spielereien

Zurück zur Startseite

Kai Schröder, 29.11.2000